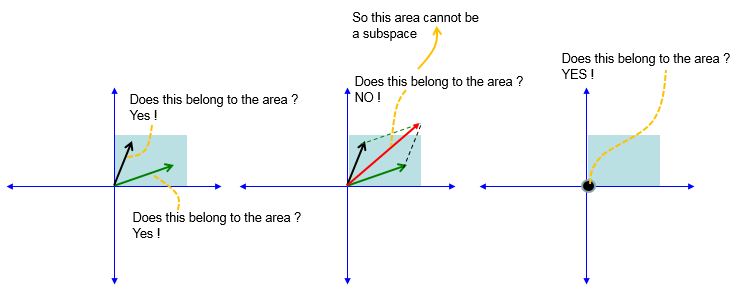
Subspace Of A Vector Space

Q ⊆ ( ℝ n int undefined H ) ¯By contradiction, let us suppose that there exists a point y ˜ ∈ ( int undefined H ∩ K 2 ¯ ). Then the angle ∠ x 0 y 0 y ˜ is less than π / 2, and, besides, since conv K 2 is convex, it follows that y 0, y ˜ ∈ conv K 2.

Let us take the point y ˜ ′ ∈ ( y 0, y ˜ ) such that ( x 0, y ˜ ′ ) ⊥ ( y 0, y ˜ ) and show that y ˜ ′ is not a point from conv K 2 close to x 0. Indeed, the points y 0, y ˜ and y ˜ ′ belong to the same line and y ˜ ′ ∈ int undefined H. But, if y ˜ ′ ∈ y 0, y ˜ and y ˜ ′ ∈ conv K 2, then obligatory ‖ x 0 − y ˜ ′ ‖. (10) 〈 T f, φ 〉: = ∫ f ( x ) φ ( x ) d x, φ ∈ D ( Ω ),is, in fact, a distribution from D' (Ω). The mapping L l o c 1 ( ℝ ) → D ′, given by f ↦ T f is injective, i.e., if f, g ∈ L l o c 1 ( ℝ ), then T f = T g if and only if f = a.e. G.The distributions of the type T f, i.e., defined with a function f ∈ L l o c 1 ( ℝ ) by (10), are called regular.

A typical example of a non-regular (or: singular) distribution is the delta distribution given by (7), and also its generalization, the functional δ a, a ∈ Ω, given. Σ k = 1 n λ k x α k = 0,then, forming the inner product of each side of this equation with x α j, we should have λ j x α j 2= 0.It is easy to obtain an orthonormal system from an orthogonal one by dividing each element by its norm (assuming that the system does not contain the zero element).

Going from an arbitrary system of elements to an orthonormal one is more complicated. Restricting ourselves to the case of a countable system, we next prove the following orthogonalization theorem (due to Schmidt). Where σ 2 is the noise variance. Noise reduction in Weyl-Heisenberg and wavelet frames in L 2(ℝ) was also studied by Daubechies 4, under the same assumption of a white, additive, zero-mean noise. Suppose that a signal f ∈ L 2(ℝ) is well localized in a bounded region of the time-frequency plane, so that it can be well approximated using a finite number of elements of a wavelet or Weyl-Heisenberg expansion (those localized in the same region).

If the expansion coefficients f φ ˜ j j ∈ J are subject to the noise n j j ∈ J then f can be reconstructed as. In, 1970 7.5. Failure of the Hahn-Banach TheoremWe have just seen that H p has enough continuous linear functionals to distinguish elements of the space, even if p. ∑ n = 1 ∞ n γ b n 2 = ∞ for each γ 0,unless g = 0. But this contradicts Lemma 3, since g ∈ Λ α.We remark that SH p is a proper subspace unless S = 1.

Corollary 1If S is a singular inner function as described in the theorem, the quotient space H p/( SH p) has no continuous linear functionals except the zero functional, for each p.

One-dimensional subspaces in the two-dimensional vector space over the F 5. The (0, 0), marked with green circles, belongs to any of six 1-subspaces, while each of 24 remaining points belongs to exactly one; a property which holds for 1-subspaces over any field and in all. All F 5 2 (i.e. A 5 × 5 square) is pictured four times for a better visualizationIn, and more specifically in, a linear subspace, also known as a vector subspace is a that is a of some larger vector space. A linear subspace is usually called simply a subspace when the context serves to distinguish it from other types of subspaces. Finite-Dimensional Vector Spaces. Princeton, NJ: Princeton University Press.

It's a real special place. It never rains—but the crops don't die. Food grows free, neighbors smile, and the animals are happy to see you. HAY DAY—IT'S 100% FREE-RANGE FUN! Hay Day is free to download and install. However, some game items can also be purchased for real money. If you do not want to use this feature, please set up password protection for purchases in. Hay day game download apk. Hay Day lets you get back to nature and experience the simple life of working the land. It’s a special game set in a real special place. Food grows free, people smile and the animals are always happy to see you. It never rains here, but the crops never die. And if you’re craving a little bacon, one of the pigs will be happy to fry some up.

P. 14. The term linear subspace is sometimes used for referring to. In the case of vector spaces over the reals, linear subspaces, flats, and affine subspaces are also called linear manifolds for emphasizing that there are also., p. 155)., p. 176)., p. 132)., p. 200)., p. 20). See Paul DuChateau. Retrieved September 17, 2012. For. Generally, K can be any field of such that the given integer matrix has the appropriate in it.

All fields include, but some integers may equal to zero in some fields. This definition is often stated differently: vectors v 1., v k are linearly independent ift 1 v 1 + + t k v k ≠ 0 for ( t 1, t 2., t k) ≠ (0, 0., 0). The two definitions are equivalent., p. 21)., p. 20)., p. 21)., p. 22)., 6.46., 6.50., 6.47., 6.51.Textbooks. Anton, Howard (2005), Elementary Linear Algebra (Applications Version) (9th ed.), Wiley International. Axler, Sheldon Jay (2015), Linear Algebra Done Right (3rd ed.), Springer-Verlag,. Beauregard, Raymond A.; Fraleigh, John B. (1973), Boston:,.

A subspace is a vector space that is contained within another vector space. So every subspace is a vector space in its own right, but it is also defined relative to some other (larger) vector space. We will discover shortly that we are already familiar with a wide variety of subspaces from previous sections. Let F be a field and n a natural number. Then Fn forms a vector space under tuple addition and scalar multplication where scalars are.

Herstein, I. (1964), Topics In Algebra, Waltham:,. (1972), (3rd ed.), New York:,. Lay, David C. Dream high ep 10 eng sub. (August 22, 2005), Linear Algebra and Its Applications (3rd ed.), Addison Wesley,. Leon, Steven J.

(2006), Linear Algebra With Applications (7th ed.), Pearson Prentice Hall. Meyer, Carl D. (February 15, 2001), Society for Industrial and Applied Mathematics (SIAM), archived from on March 1, 2001. Nering, Evar D. (1970), (2nd ed.), New York:,. Poole, David (2006), Linear Algebra: A Modern Introduction (2nd ed.), Brooks/Cole,External links., at Google Video, from.